Fit to the longitudinal growth curve by the Wavelet

Katsunori Fujii

　　　　 Abstract

Fit to the longitudinal growth data by the WIM is discussed in comparison with previous mathematical functions. General logistic function and spline fitting method were respectively applied to one set longitudinal height growth data from 6 to 17 years as the previous mathematical functions. Goodness of fit to the longitudinal growth data in the both methods was compared with the WIM. In the comparison between the WIM and spline fitting method, accuracy of the fit to growth amount during a year( increments in height from year to year ) in the both methods was discussed because it is difficult to compare the goodness of fit to the growth distances. As the results, advantages of the WIM was demonstrated, and the WIM was applied to longitudinal height growth record from 6 to 17 years of Montbeillard's son. Biological parameters were easily identified, and second event ( mid-growth spurt ) before age at MPV( the peak during adolescence) was derived from the graph described by the WIM.

　　緒　言

　 ウェーブレット（ Wavelet ）とは元来「小さな波 」あるいは「さざなみ」を意味する言葉である。工学分野では、振動や波動を扱う場合、局所的な振動波形を表す用語として古くから用いられてきた。現在のウェーブレット理論は、１９８０年代初頭にＪ，Ｍｏｒｌｅｔ(1983)が考えた(wavelet of constant shape)を使った新しい時間周波数解析に始まるとされている。彼は石油探査のために全く新しい発想として、一つの波を拡大縮小できる短い波、つまり、 Wavelet を考え出したのである。そして、この発想がＭｅｙｅｒ(1993)により、数学の分野として抽象的枠組が整えられ、積分変換の離散化が試みられ、滑らかなウェーブレットによる完全正規直交基底を組み立てることに成功したのである。

　 このような中で、筆者(1995)(1996)はウェーブレットを成長学に導入した訳だが、その背景には成長現象解明のために、数学的関数による曲線の記述が構成されてきたこと、それと、成長現象が年齢という時系列によって構成されることに端を発していることと考えられる。しかし、このような理由であれば、ロジスティック系の関数やスプライン関数でもいいわけで、故ウェーブレットでなければならないのか。それは、”真の成長曲線とは何か”という命題に一つのアプローチを得た事である。つまり、東郷(1982)(1988),小林と東郷(1993)によって示されたように、毎日の成長記録は小刻みな波動を示すが、その波動はある大きな波を形成する。この現象は考え方によれば、ある種の相似現象ではないだろうか。つまり、年齢軸を限りなく小刻みにしていっても、同じ波形が繰り返えされるという現象で、言い替えれば、自然界に存在するフラクタル現象ということである。その立証はともかくとして、このような現象を表現できる数学的関数は、フーリエ級数（解析）が考えられるが、その発展的拡張がウェーブレットであり、したがって、成長現象のフラクタル性を表現できる数学的関数としてこのウェーブレットが考えられ、このような発想がウェーブレットと接点を持つに至った訳である。したがって、今回はウェーブレット解析を成長現象に適用し、真の成長曲線の近似として表現出来ることを示すものである。

　方　法

　1. ＷＩＭの数学的意義

　 通常時系列を扱う場合、フーリエ解析が良く知られている。多くの場合、ＦＦＴなどを用いて基のデータをフーリエ変換し、フーリエスペクトルを描いてみることで、主要な周期の同定が行われる。の場合、周期性の検出にはフーリエ変換の積分核であるｅ^ｉｗｔという関数が周期関数であることにある。また、周期性とは別の用途にフーリエ 変換を用いる場合、データに含まれる相似性を検出する道具としてのフーリエ変換である。通常、データの時系列が自己相似的な構造を持っている場合、スペクトルの形はべき関数となる。このようにフーリエ解析は周期性と相似性の検出に優れている。しかしながら、いつもフーリ解析が便利なわけではない。フーリエスペクトルはフーリエ変換の位相部分を消去した量で時刻に関する情報を失っているため、スペクトルと局所事象との対応関係を見い出す事ができない。そこで、このような欠点を克服するためにウェーブレット解析が提唱された。つまり、データの持つ局所相似性の解析には最適であり、特に、スペクトルのべき則を伴う現象の解析やデータ関数の各点毎の特異性強度の検出には非常に有効といえる。このように、今まで述べてきた事は数学的な理論的根拠に基づく事実であり、明確なウェーブレット解析の有効性を示す解釈といえる。このことを数学的に端的に示すと以下のようになる。

(1-1)

　 上式は一般的なフーリエ級数である。この式をオイラーの公式に従って変形すると以下の式になる。

(1-2)

　 上式から理解されるように、関数の異常性（不連続性）等はフーリエ係数ｃ_ｎの減衰オーダーに反映されているとはいうものの、その異常性を正確につきとめることはできない。この異常性を正確につきとめるためには上式に時刻のパラメーターを加える必要がある。実はその発想がウェーブレットになるわけである。今、２つの実数パラメーター ａ，ｋを用いて作られる特殊な関数Ψ（ｘ）を(1-3)とする。

(1-3)

上式から分かるように、元の関数（通常はmother waveletと呼ばれている）Ψ(ｘ）を横軸にａ倍、縦軸に倍それぞれ拡大した後、さらに横軸にｋだけ平行移動させたものである。フーリエ級数と根本的に違う点は時刻のパラメーターとしてのｋが設定されていることにある。すなわち、ウェーブレットとは基本的に相似的変形と平行移動によって得られる一群の関数のことである。

　 さて、ここでやみくもにウェーブレットを集めても実用にはならない。通常、実用のために旨く離散化すると以下の式になる。

　　(1-4)

　上式はウェーブレット展開式で、実用として用いる場合は２のべき乗としている点である。ｊはスケール、 ｋは位置 （時刻）のパラメーターである。通常、実用化としてはこの式が適用されるが、具体的な演算に際してはさらに複雑な式になる。

　 以上の数学的説明は、一般的にはスペクトル解析に適用されるが、成長曲線記述に対する発育学的意味を与えているわけではない。そこで、成長曲線記述に対して適用される形としては、データとデータの間を滑らかに補間することが必要であり、そのための補間アルゴリズムをウェーブレット補間法という形で以下に示す。

　２.　ＷＩＭの数学的アルゴリズム

２−１．多重解像による分析

時系列解析の立場からは、個々人の身長（体重等）の記録は時間に関する連続曲線とみなされる。したがって、身長に関する成長曲線の分析は滑らかな関数の集まり（これを数学では関数空間という）を解析することと同じことになる。このような滑らかな関数を含む関数空間の中で最も基本的なものに二乗可積分関数による Ｌ２（Ｒ）-空間がある。多重解像の立場から（Meyer(1992), Mallat(1989)）この Ｌ２（Ｒ）を部分空間の和に分解できる。

(2-1) Ｌ２（Ｒ）＝ ・・・＋Ｗ−１＋Ｗ0＋Ｗ１＋Ｗ２＋・・・

　　　　 Ｌ２（Ｒ）は互いに直交する部分空間Ｗｎに分解できる。

(2-2) Ｗｎ＝｛Ψ( 2nt - k )：ｋは整数｝ ：ｎ＝０，±１，±２，・・・

　　　　 部分空間Ｗｎは１つの関数（これをウェ−ブレットという）Ψ(t)の時間を移動し

　　　　 た関数から作られる。

(2-3) ｆ（ｔ）∈Ｗｎ ⇔ ｆ（２ｔ）∈Ｗｎ＋１

　　　　 各部分空間は時間を拡大縮小することにより、他の部分空間に移ること

　　　　 ができる。

このことより、任意のＬ２（Ｒ）- 関数Ｆは (2-4) と直交展開でき、これを ウェーブレット級数という。

(2-4) ： ただし、ｎ，ｋは整数とする。

基本となるウェーブレットにはsupport compact なDaubechies 関数 (1992)やスプライン、Wavelet など数多くの関数が知られている。本論文では滑らかな ウェ−ブレットを必要とするため、Meyer Wavelet(1992)を構成し、利用する。

　２−２．ウェ−ブレット補間法（ＷＩＭ）

　 身長などの発育曲線は滑らかなＬ２（Ｒ）- 関数Ｆ(t) と表せることを仮定する。この発育曲線Ｆは多重解像によりウェーブレット級数 (2-4) として表現できる。

我々が提唱するＷＩＭ ( Wavelet Interpolation Method ) は、観測データと一致し、各データの間を補間し、その上、Ｆ(t)の近似となっている関数を求め、Ｆの時間微分である発育速度曲線の peak の性質を調べる方法である。

ＷＩＭの手順は以下の通りである。

( 1 ) 測定デ−タ {(tｉ,yｉ):i=1,2,・・・,11} を得る。

（ここでは、ｔｉは年齢、ｙｉは体格項目の現量値とする）

( 2 ) Meyer Wavelet ψ(t) と ψ'(t) を構成する。

( 3 ) Meyer Wavelet を次の条件を満たすように修正する。

　 t<0 または t>1 のとき、｜ψ(t)｜≦ ε. （ε=0.01 にとる）

( 4 ) 次の条件を満たす 11 個の整数の組 (j,k) を決定する。ただし、ｊ≦１． 　 　 　　　　　 ｜ψ( 2jti - k )｜≦ε　

( 5 ) 観測デ−タから Wavelet functionψ( 2jti - k ) を係数とする連立方程式の解としてウェ−ブレット係数 { ajk ; j,k} を求める。

・・・

( 6 ) ( 5 ) で求めた {aj,k ; j,k} を係数とする近似関数 Ｆｎ ，ｆｎ のグラフをコンピュ−タで描く。

( 7 ) 近似曲線のシミュレ−ションから導関数 ｆｎ(t) の極値であるＭＰＶの時点 ｔ を特定する。

( 8 ) ＭＰＶ以外のピーク値、すなわち mid-growth spurt, after-growth spurtの時点 ｔをグラフから特定する。

　３. ＷＩＭの有効性について　

　筆者の先行研究(1995)(1996)によって、３次多項式をＷＩＭがそのまま表現することが可能であることを示し、さらに、６つの数学的関数に対しＷＩＭとspline関数を当てはめ、その当てはまりの精度を両者で比較した結果、関数の微分に対する当てはまりの精度が、明らかにＷＩＭの方が高いことが示された。このことはＷＩＭによって導かれる速度曲線の有効性が保証されたことになると考えられるが、しかし、生物学的意味における有効性を示しているわけではない。そこで、実際の観測データから得られた身長の縦断的測定値に対し、従来から適用されてきた数学的関数としてｌｏｇｉｓｔｉｃ関数およびcubic spline関数を当てはめ、ＷＩＭとの精度を議論する。

Example １ : ｌｏｇｉｓｔｉｃ関数とＷＩＭの比較論議

　 以下に示された身長の観測データに対してＷＩＭとｌｏｇｉｓｔｉｃ関数を当てはめた。

(1-1)と(1-2)式は当てはめられたｌｏｇｉｓｔｉｃ関数式の元の関数と一次導関数である。

( 1 - 1 )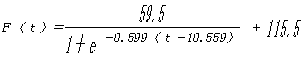

( 1 - 2 )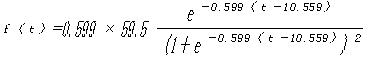

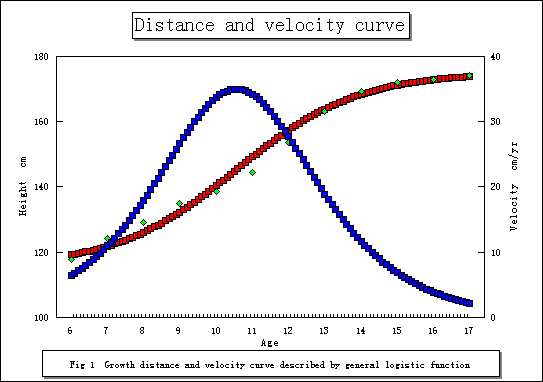
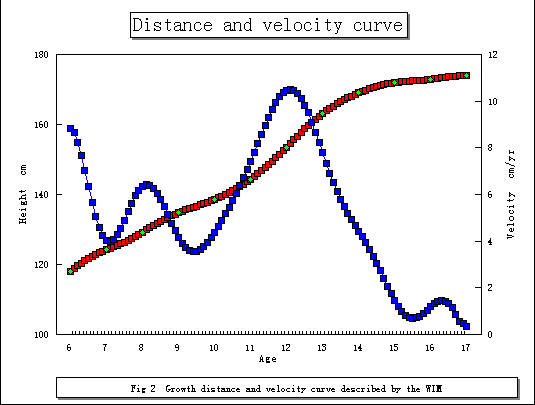
そして、この式から導かれたグラフが Fig 1 であり、ＷＩＭによって導かれたグラフがFig 2 である。

Observed longitudinal height growth data

　 グラフから明らかなように、ｌｏｇｉｓｔｉｃ関数による発育現量値への当てはめは、観測データ点を通過していないが、ＷＩＭは観測データ点を通過するように構成されているため、精度の議論からすれば当然ＷＩＭの方が優れているといえる。そして、速度曲線としての両者の微分曲線を比較すると、ｌｏｇｉｓｔｉｃ関数の対象的な山形の曲線に対して、ＷＩＭでは思春期ピーク以外の二次的ピークの事象まで検出している。このようなことから、ＷＩＭは生物学的意味において、ｌｏｇｉｓｔｉｃ関数よりも優れていると考えられる。

Example 2 : ＷＩＭとspline 補間法との比較論議

　 Example 1の場合と同様に、以下の観測された身長の縦断的発育データに対して、ＷＩＭとcubic spline を当てはめた。その結果、両手法により描かれたグラフはFig 3, Fig 4である。グラフから肉眼で判断する限り、両者の差異は明確には示されていない。時に、発育現量値曲線に関しては、両手法とも観測データ点は通過できるように構成されているため、当てはめの精度を議論するすることは難しい。しかしながら、速度曲線としての一次導関数の曲線を評価することは可能である。つまり、観測された生のデータから導かれる年間発育量は、唯一真の記録であり、比較議論の指標となる事実上の基準値である。したがって、年間発育量を１年間の平均発育速度とみなして、ＷＩＭとcubic spline から導かれた速度の１年間の平均値を求め、その速度量を両者において比較した。ここで、明確にしておかなくてはならない事は、cubic spline の第一次微分は二次関数であり、第二次微分は一次関数となり、成長曲線への当てはめにおいて、微分が実用にならない問題点が存在する。今回の cubic spline の速度曲線は数値微分と称する、現量値の年齢間隔を細分してその差分を採用している。もちろんＷＩＭは無限回微分可能な数学的性質を持っているため、このことからすでに有効性の理論的根拠は明確であろう。

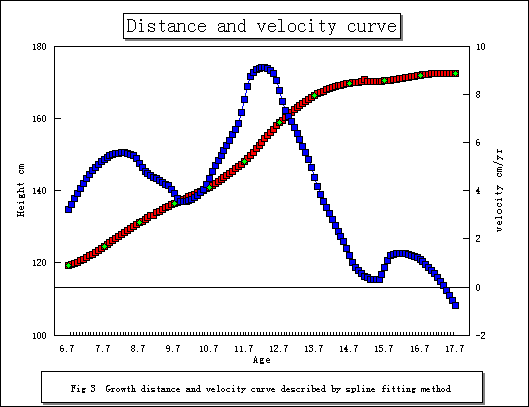
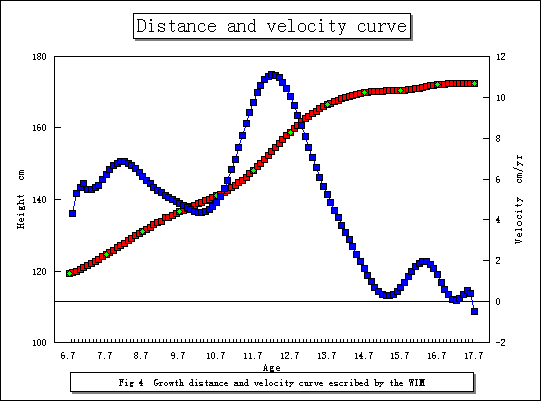
　 Table 1 は両手法によって導かれた発育速度における１年間の平均速度を計算したものである。この表からも分かるように、ＷＩＭの方が観測された生の年間発育量の数値に近いことが示されている。このことは逆に、発育現量値の補間の精度に還元されていく結果と考えられる。つまり、発育現量値への当てはめの精度が、速度曲線に対する精度の議論から評価されることになるわけである。このことから、ＷＩＭの生物学的な有効性が明確に示されたと考えられる。

Observed longitudinal height growth data

Example 3 ゲノードモンベヤールの息子の身長に対するWIMの適用について

Fig 5 はScammon(1927) の論文に掲載されたゲノードモンベヤールの息子の身長の記録をグラフにしたものである。都合上、６歳から１７歳までの１年間隔で設定してある。発育現量値曲線は年齢に対応させて、そのまま記録をプロットしたものだが、差分としての年間発育量については、グラフの作成上、年齢軸の速い方に対応させて設定してあることに留意されたい。このグラフから分かることは、思春期ピークは１４歳で示されているが、実際は１４歳から１５歳の間で、つまり、ＰＨＶ年齢としては１４．５歳ということになる。そして、その時点での速度量は１２．１cm/yrである。また、take off age（思春期スパート開始年齢）での落ち込みがかなり大きい事が分かる。しかしながら、このグラフからは概観としては理解されるが、これ以上の解析は望めない。つまり、この折れ線グラフ自体が厳密には速度を示しているわけでなく年間発育量を示しているにすぎず、速度曲線として解析するには限界があるわけである。

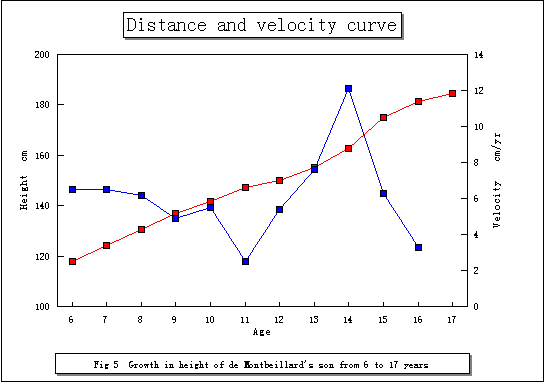
　 そこで、厳密な速度曲線として描くことができるWIMを適用した結果、Fig 6が示された。

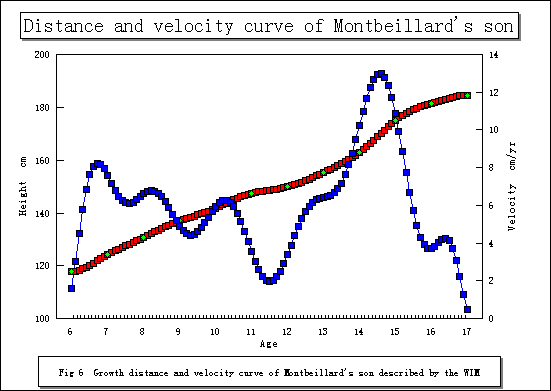
このグラフから判断すると、思春期ピーク年齢（WIMによって導かれたピーク年齢はＭＰＶ年齢と定義される。）は１４．６歳でその時点での速度（ＭＰＶ）は１２．９８cm/yrと特定された。また、この速度曲線からは発育速度の様子が明確に把握され、特に、ＭＰＶ年齢以前の二次的ピークとしてのmid-growth spurtの存在が明示されている。ちなみに、mid-growth spurtのピークは２ヶ所で出現しており、そのピーク年齢と速度量は８．２歳（6.8cm/yr）と１０．３歳（6.27cm/yr）であった。このようにWIMを適用することにより、従来までの発育速度曲線のぼやけた部分が明確化され、その部分の解析が可能になるものと考えられよう。

　結果および考察

　 Example 1〜3により、WIMの有効性は明示されたと考えられる。logistic関数との比較では、明らかに発育現量値の記述においてはWIMの精度が高いことは証明されたわけであるが、この議論の要点は当てはめられた関数値の観測データ点に対する誤差の大小によって判断されることで、その意味からすれば、観測データ点をすべて通過できるように構成されたWIMの方が当然有効であると言える。したがって、logistic系の関数（double logistic, triple logistic, Preece and Bain(1978)モデルの複合logistic関数）についても、少なくとも観測データ点をすべて通過していないことを考えれば、logistic関数の比較の場合と同様の判断ができるのではないだろうか。

　 しかし一方で、必ずしも観測データ点を通過する必要はないのではないかという考え方もある。確かに標準モデルを構築するための記述の手法であれば、観測データ点を通過させる必要はないかもしれない。ならば、何故観測データ点に対する誤差を議論する必要があるのか。このような誤差の議論が観測データ点を必ず通過することを要求したのではないだろうか。いずれにせよ、観測データ点を通過することが、第一次微分である速度曲線を忠実に描くことに反映されるものと言えよう。

　 sｐline関数との比較論議では、両手法とも発育現量値の観測データ点は必ず通過できるように構成されているため、現量値に対する精度の比較は困難である。そこで、速度曲線に対する精度を議論した訳であるが、もともとspline関数は元のデータに対する滑らかな補間が目的であり、微分は区分内においては可能であるが、元の関数が３次多項式であるために、第１次微分が２次多項式、第２次微分が１次関数となってしまう。したがって、基本的には微分は実用にならないとされている。今回、spline関数の速度として算出してあるのは、数値微分と称する差分を適用している。つまり、数学的には微分ではないので速度として扱えない問題がある。しかし、一応spline関数の速度として論議したが、結果的には年間発育量に対する精度はWIMに方が高いと判断される。そして、この精度の議論から、逆に判断して発育現量値に対する精度もWIMの方が高いと言えよう。

　 今回、spline関数との比較において、年間発育量に対する誤差を議論したのは今までにない試みである。したがって、この議論の妥当性を判断する客観的な指針はない。しかし、いずれにせよ、唯一、真の事実である年間発育量を判断の対象とすることは妥当な試みと言えるのではないだろうか。

　 以上、ＷＩＭの有効性を踏まえながら、モンベヤールの息子の身長に対してＷＩＭを適用した。その結果、描かれたグラフ（ Fig 6 ）は観測されたデータをプロットした折れ線グラフと比較すれば、当然滑らかに描かれており、速度曲線の様子は明確に把握される。したがって、発育学的パラメーター（思春期ピーク年齢、その時点での速度量、take off age等）が容易に特定することができる。特に、折れ線グラフでは把握されにくい思春期ピーク年齢の前に出現する二次的ピークであるmid-growth spurtが示されていることである。この事象の議論についてはここでは触れないが、WIMがこのような事象を検出し易い手法であることは理解される。また、Gasser(1984)(1985),松浦(1991)によって指摘された思春期ピーク年齢の後に出現する二次的ピーク（after-growth spurt:松浦によって名付けられた）の存在についても、このグラフには示されていないが、WIMによって他の多くの身長のデータで確認されている。このように、WIMを適用することにより発育曲線の解析の範囲がより拡大されていくものと思われる。

　参考文献

1. Daubechies, I. ( 1992 ) Ten Lecture on Wavelets, SIAM Philadelphia.

2. 藤井勝紀, 川波憲一, 長谷川泰洋, 山本浩 ( 1994 ) Wavelet 解析による身長発育の時系列　 分析. 発育発達研究 22 : 21-28.

3. 藤井勝紀, 山本浩 ( 1995 ) 身長の成熟別発育速度曲線の解析. 体力科学, 44 : 431-438.

4. 藤井勝紀, 山本浩. ( 1995 ) Wavelet Interpolation Method による男子体重発育におけるＰＨＶの検討. 発育発達研究　23 : 27-34.

5. Fujii, K. and Yamamoto, Y. ( 1995 ) Wavelet Interpolation Method for time series analysis in the growth and development study. Nagoya Journal of Health, Physical Fitness and Sports, 18 : 13-17.

6. 藤井勝紀, 松浦義行. ( 1996 ) 男子体格の平均発育曲線から導き出される速度曲線の解析.

体育学研究　41 : 247-260.

7. Gasser, T., Kohler, W., Muller, H. G. and Kneip, A. ( 1984 ) Velocity and acceleration of height growth using kernel estimation. Ann. Human Biol, 11 : 397-411.

8. Gasser, T., Muller, H. G., Kohler, W., Prader, A., Largo, R. and Molinari, L. ( 1985 ) An analysis of the mid-growth and adolescent spurts of height on acceleration. Ann. Human Biol, 12 : 129-148.

9. Kobayashi, M. and Togo, M. ( 1993 ) Twice-daily measurements of stature and body weight in two children and one adult. Amer. J. Human Biol, 5 :193-201.

10. Mallat, S. ( 1989 ) Multiresolution Approximations and Wavelet Orthonomal Bases of Ｌ２（R）. Trans of Amer Math Soc, 315 : 69-87.

11. Matsuura, Y. ( 1991 ) A study on physical growth and development through investigating the polynomial fitted their distance curves : in the term over 6 and 18 years old. Bull. J. of Health and Sports Sciences, University of Tsukuba, 14 : 201-210.

12. Matsuura, Y. and Kim, M. ( 1991 ) Analysis of physical growth by fitting the polynomial to the longitudinal growth distance data of individual: age 6 to 17. Research Monograph issued by Growth and Development Research Institute of Health and Sports Sciences, University of Tsukuba. pp. 1-153.

13. Meyer, Y. ( 1992 )　Wavelets and operators. Cambridge University Press.

14. Morlet, J. ( 1983 ) Sampling theory and wavelet propagation, in NATO ASI Series ,Vol.1 ,Issues in Acoustic signal/Image processing and recognition, C. H. Chen, ed., Springer-Verlarg, Berlin, pp. 608-616.

15. Preece, M. A. and Baines, M. J. ( 1978 ) A new family of mathematical models describing the human growth curve. Annals of Human Biology. 5 : 1-24.

16. Togo, M. and Togo, T. ( 1982 ) Time-series analysis of stature and body weight in five siblings. Ann. Human Biol, 9 : 425-440.

17. Togo, M and Togo, T. ( 1988 ) Initiation time of adolescent growth spurt estimated by a certain through in time - series analysis of monthly anthropometric and urinalysis data in five siblings. Human Biol, 60 :223-235.